Computational Geodynamics Primer
Understanding Earth’s Dynamic Processes Through Mathematical Modeling and Computation
Overview
Our goal is to develop a quantitative understanding of the dynamic processes within the Earth and sister planets. These dynamic processes are largely driven by the internal heat of the planet escaping to the surface through whatever mechanisms are available. Some of the heat is left over from the original formation of the planet, and the rest originates in the decay of radioactive elements. In the Earth’s early history and elsewhere in the solar system, tidal heating, chemical segregation, and impacts have all played a role in supplying the interior heat budget.
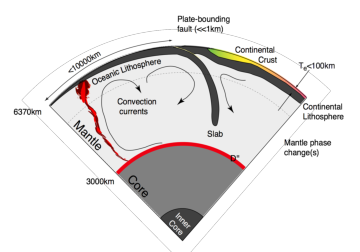
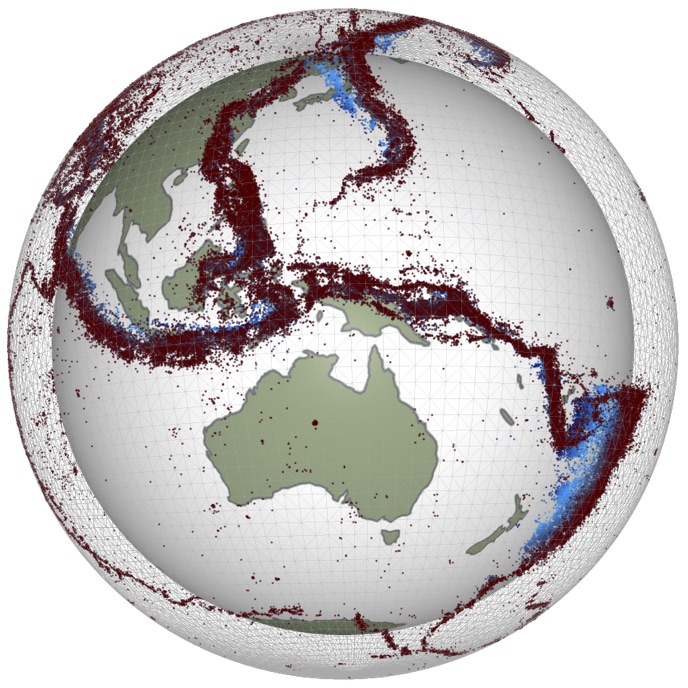
This is because the Earth’s dynamics is completely dominated by Plate Tectonics — a unique manifestation of interior heat loss as far as we are aware. Understanding why plate tectonics is a possible outcome of a hot planet, and also why it is not the only possible outcome, is one of our key tasks. If we can understand how different dynamic modes are selected for planets of different size, composition, and heat budget, then we have a powerful way to predict the geological behaviour of extrasolar planets. Plate tectonics creates efficient cycling mechanisms which link the interior of the Earth with the Atmosphere and Oceans; it may prove essential for sustaining life.
What is a Model?
Global-scale geodynamics is a discipline where we cannot do controlled experiments on the basic processes we are studying. Instead, we rely on observing the Earth and other terrestrial planets and moons, and looking for multiple manifestations of the same processes under different conditions to give us control on certain parameters.
While it is not possible to do experiments at the planetary scale over geological time, it is possible to perform experiments at a physically manageable size and, by careful scaling, to generalise the results to geologically relevant space and time-scales. If these processes of interest can be understood through a mathematical description, then the equations are automatically applicable at geological time and space scales provided the assumptions which go into developing the mathematical model are still valid.
When we talk about “modeling” in geodynamics, we mean several related but distinct things:
- Laboratory-based physical models which can be scaled to give meaningful, quantitative insight into deformation at geological scales.
- Mathematical descriptions of the world and their use to approximate physical reality.
- Computational solutions of these descriptions (where needed) and the concept of a numerical model.
- How to construct a model
- How to use a model (these are quite different things!)
- Exploring parameter variation to understand dominant effects.
Mathematical Background
These notes contain material at different levels. There is broadly descriptive content which introduces the subject and leads up to more advanced mathematical material. It should be possible to follow these notes without detailed knowledge of how the mathematical results are obtained, but it is expected that you can use the results to solve real problems in geophysics.
Familiarity with vector & tensor notation and index notation is required for understanding the kinds of equations we will be dealing with. We interchange these notations and tend to write everything out in full for the Cartesian case. In other geometries, vector notation generally still holds, but the definition of the operators can be very different, and it is always worth checking before using them.
Programming in Python
All of the examples in this book are based around Python code, which is easy to pick up and very powerful. Many Python codes are actually Fortran or C codes in disguise, with Python providing a more convenient way to operate and coordinate programs than older approaches.
Python is a very flexible language which is constantly improving. The flexibility can make it hard to know where to start or how to find documentation. Jupyter notebooks add interactivity to Python and make it much more straightforward to dig into the details of the code you are running. We use Jupyter notebooks extensively for examples in this book, and these can be run live using browser-based Python (pyodide) or online Jupyter environments (Binder).
Book Structure
This book is organized into five main parts:
Part I: Mathematical Fundamentals
The mathematical tools you need to understand geodynamics, including vector and tensor notation.
Part II: Fluid Dynamics
The foundations of fluid mechanics and flow dynamics that govern mantle and planetary fluid motion.
Part III: Geodynamics
Applications of fluid dynamics to planetary processes including mantle convection, plate tectonics, and lithospheric dynamics.
Part IV: Numerical Methods
The computational techniques needed to solve the mathematical equations describing geodynamic processes.
Part V: Computational Exercises
Practical examples and benchmarks demonstrating the concepts throughout the book.